Nuclear Reactions
Mathematically Modeling Nuclear Reactions
pynucastro is open-source and freely available at the pynucastro GitHub.
Nuclear physics powers a vast array of high energy astrophysics events, from fusion in stars to supernovae and neutron star dynamics. Nuclear reactions between atomic nuclei within stellar environments generate energy for starlight and power hydrodynamics and observable radiation.
We model nuclear energy generation with rate equations that couple nuclei via nuclear reactions at high temperatures. In turn, nuclear physicists assemble theoretial cross-sections and available experimental data from particle accelerators to calculate the nuclear reaction rates at various astrophysical temperatures.
I worked with Mike Zingale to create pynucastro, an open-source Python package for interfacing with nuclear reaction databases. With pynucastro, researchers and students alike can easily:
- plot nuclear reaction rates
- assemble nuclear reaction networks specific to the astrophysics conditions they wish to model
- solve the nuclear reaction equations
- output clear C++ or python code to calcuate nuclear reaction models in other astrophysics simulation codes
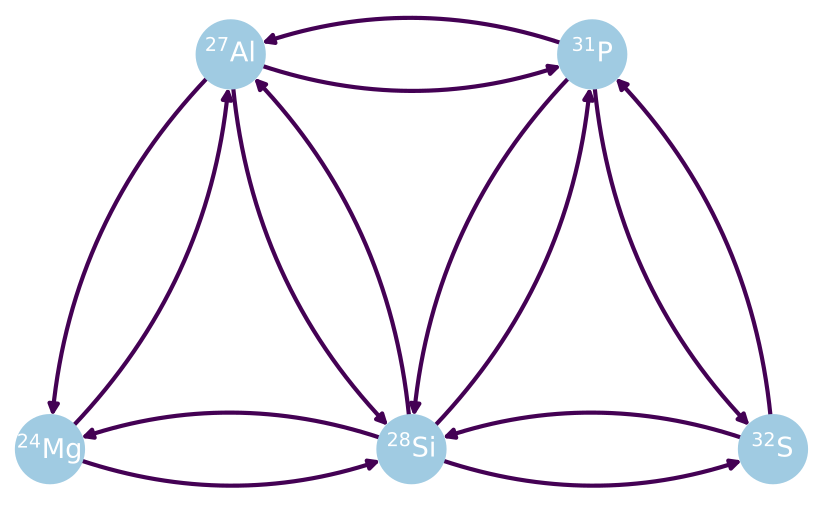
For details, see E. Willcox & Zingale (2018) and Smith et al. (2023).
Computationally Solving Nuclear Reactions
Our Microphysics solvers are open-source and freely available at our Microphysics GitHub.
Nuclear reaction equations actually look mathematically similar to rate equations for chemistry. We can solve any equations of this sort using a variety of time integration techniques for coupled, first order ordinary differential equations. However, nuclear reactions pose a particular challenge in that they are very stiff, nonlinear equations due to their extreme temperature dependence.
Physically, this extreme nonlinearity arises because the probability of fusion tunneling through the nuclear Coulomb barrier increases sensitively with the center of mass energies of two nuclei. As astrophysical plasmas reach higher temperatures, nuclei within the plasma reach larger center of mass energies for pairwise interactions. High temperatures thus generate much more likely fusion events.
Nuclear reactions are thus especially sensitive to temperature, after all, that’s why stars can explode in thermonuclear runaway! This extreme temperature sensitivity makes numbers in our equations tend to “blow up” quickly too, so we have to take small, careful arithmetic steps to solve these equations correctly.
In mathematical terms, we have to use implicit time integration with careful error control. All such techniques achieve accuracy by implementing more careful calculations. Careful calculations and good error control require additional arithmetic steps, so we need more computing resources to make accurate predictions. While the accuracy versus efficiency tradeoff is especially prominent in nuclear astrophysics, virtually all other fields in computational science struggle with this exact tradeoff.
(If you’ve ever wondered why meteorologists can get weather predictions wrong, well, it’s likely their predictive calculations traded too much accuracy for efficiency!)
Note that if we carelessly write simulation code, even the fastest supercomputers will simply give us wrong answers fast!
For a discussion of the subtleties of solving nuclear reactions with some common methods, see Zingale et al. (2021).
To take advantage of modern heterogeneous supercomputers with lots of GPUs, I ported the VODE solver for implicit time integration from Fortran 77 to CUDA Fortran. But I realized there could be no room for mistakes, so I followed the old adage - “trust but verify.”
In my case, I spent every effort to accurately port a highly complex code. Anyone who has ever had to trace the combinatoric pathways of nested go to statements will sympathize!
But I didn’t fully trust that I had made no mistakes or that the GPUs would yield correct answers. So I carefully verified the code, requiring that it give me exactly the same results as before the port when comparing CPU calculations. When running my new code on the GPUs, I allowed its results to differ from the CPU results only at the level of numerical roundoff error.
Our collaboration described this port and the science our combined reaction and hydrodynamics code enabled us to investigate in our paper for Supercomputing 20 Katz et al. (2020).
Later, we ported my CUDA Fortan integrator to inlined CUDA C++.
We now use generic macros from the AMReX framework allowing us to compile the same C++ integrator for CPUs, NVIDIA GPUs, or AMD GPUs.
We published our work and our open-source scientific computing codes in a series of papers.
For details, see Zingale et al. (2018), Fan et al. (2019), Almgren et al. (2020), Zingale et al. (2020), and Harpole et al. (2020).
While we directly communicated our methods and open code to the wider astrophysics community, our GPU strategy is broadly applicable to related challenges all across computational science.